This is the solution to Quiz 3: Problems - MATLAB branching, functions.
The following figure illustrates the grade distribution for this quiz.
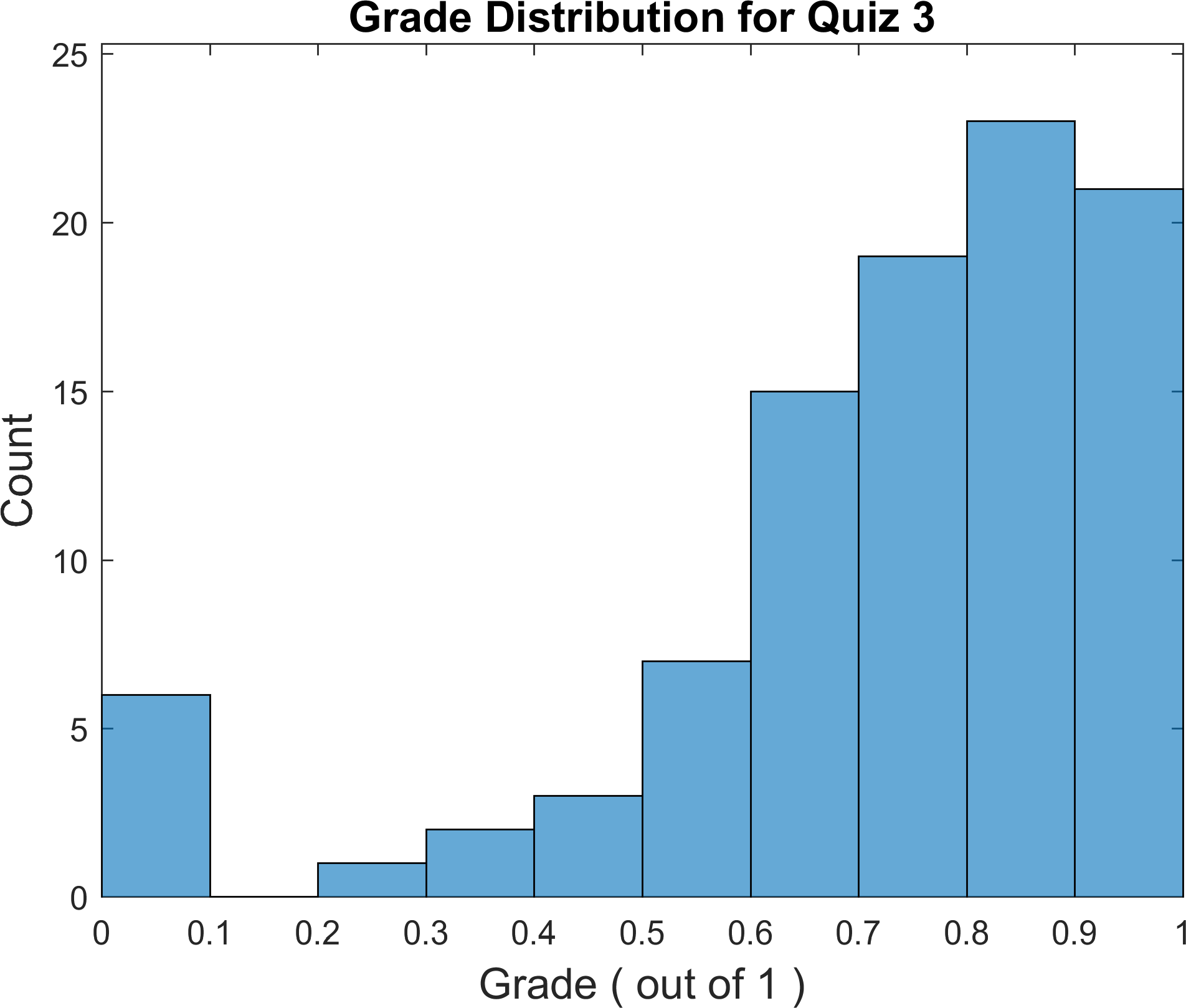
This quiz is about branching, if blocks and functions in MATLAB.
1. Describe, with an example MATLAB script, the difference between * and .* operators (basically what is the role of . in the later operator? (Hint: describe your answer by multiplying two matrices with each other.)
Answer:
The .* multiplies two arrays A and B element by element and returns the result in C, if C = A .* B. By contrast, the operator * is understood by MATLAB as matrix multiplication (or cross product). For example,
>> A = [1 0 3];
>> B = [2 3 7];
>> C = A.*B
C =
2 0 21
2. Vector Dot-Product Vector dot-product in algebra is defined as the summation of the product of the elements of two vectors of the same size. For example,
where $\sum$ denotes summation notation and $n$ is the number of elements of the vectors. Now, given your current knowledge of mathematical operators in MATLAB, what is the simplest way to get the result of the following dot-product of the two vectors $A$ and $B$,
Answer:
We discussed in question 1 above, that the operator * in MATLAB performs matrix multiplication. So, all you need to do is to convert the vector B to a column vector using the transpose operator ', in order to get the dot-product result,
>> A = [1 0 3];
>> B = [2 3 7];
>> C = A * B'
C =
23
3. (A) Write a MATLAB function named testString that takes as input, a string and then checks if the input string by the user is the equivalent to 'MATLAB’. If it is the correct string, then returns logical value true as the function output, otherwise it returns false. Provide two tests of your function which result in true and false output.
Answer:
Here is an implementation.
>> testString('MATLAB')
ans =
1
>> testString('matlab')
ans =
0
(B) One can argue that there are two basic ways of comparing two strings in MATLAB. one is using == operator, and the other is with the use of a MATLAB built-in function that we have repeatedly used in our lectures and homework. What is this function, and what is its difference with == operator. If you don’t remember this function’s name, then at least you should be able to explain the major flaw with string comparison using ==. Explain it with an example MATLAB script.
Answer:
The MATLAB built-in function for string comparison is strcmp(). This is the correct way of string comparison. The logical == operator is an elemental function, meaning that it assumes the two string being compared are arrays of characters, and therefore, the output of the comparison is also an array of logical values. For example,
>> '1' == 'amir'
ans =
0 0 0 0
>> '12' == 'amir'
Error using ==
Matrix dimensions must agree.
>> strcmp('1','amir')
ans =
0
>> strcmp('12','amir')
ans =
0
>> strcmp('amir','amir')
ans =
1
>> 'amir' == 'amir'
ans =
1 1 1 1
4. If you recall from the lectures, MATLAB has two operators corresponding to logical operator OR: | and ||. There are two minor differences between the two if you recall from our discussions in class. One is about code efficiency, and the other relates to whether we are operating on logical vectors or scalars. Describe which operator improves code efficiency and why. For the second difference, you could also provide an example to describe what each operator does.
Answer:
Recall from our discussions in class that || does short-circuiting, meaning that, if the first element is true, the result of the expression involving OR operator will be true regardless of the rest of the logical expression. For example, true OR x will evaluate to true whatever logical value x might have. Therefore, MATLAB has a special operator || for the logical operator OR, that avoids the calculation of the rest of the logical OR expression, if it is not needed, thus, increasing the speed of your code by avoiding unnecessary logical calculations. The second difference is that, the operator || is for scalar operations, for example, the following logical operation will lead to an error,
>> [true true] || [true false]
Operands to the || and && operators must be convertible to logical scalar values.
The correct operator for elemental logical OR operation is,
>> [true true] | [true false]
ans =
1 1
5. Recall that in MATLAB true and false are equivalent to 0 and 1,
>> true == 1
ans =
1
>> false == 0
ans =
1
Now knowing this, consider the following MATLAB calculation,
>> a = 1;
>> b = 0;
>> x = a/b>10.0
x =
1
Note that $1/0$ is mathematically undefined (but MATLAB by convention, assumes that $1/0\equiv\infty$). Suppose MATLAB’s default behavior is not what you would like to get, that is, you don’t want $x=1$ when $b=0$, but instead $x=0$. What would be the simplest change to the logical expression x=a/b>10.0 such that the result is $x=0$ whenever $b=0$.
Answer:
>> a = 1;
>> b = 0;
>> x = (b~=0) && (a/b>10.0)
x =
0
This way, the expression (a/b>10.0) will not be evaluated when $b=0$, and (b~=0) will be returned as the value of x.
6. Array of Structures vs. Structures of Arrays. Suppose you would like to store information about students in a class. You create a array of structures like the following,
>> AOS(1).grade = 20;
>> AOS(1).name = 'foobar1';
>> AOS(1).grade = 20;
>> AOS(1).name = 'foobar2';
>> AOS(1).grade = 30;
>> AOS(1).name = 'foobar1';
>> AOS(1).grade = 90;
>> AOS(1).name = 'foobar2';
>> AOS(1).name = 'foobar1';
>> AOS(1).grade = 90;
>> AOS(2).name = 'foobar2';
>> AOS(2).grade = 100;
>> AOS(3).name = 'foobar3';
>> AOS(3).grade = 85;
>> AOS
AOS =
1x3 struct array with fields:
name
grade
Alternatively, you could create a structure array for the same data, like the following,
>> SOA.names = {'foobar1','foobar2','foobar3'};
>> SOA.grades = [90,100,85];
>> SOA
SOA =
names: {'foobar1' 'foobar2' 'foobar3'}
grades: [90 100 85]
Suppose you have 10000 students in your class. Which one of these representations do you think would be more computationally efficient to represent the student data, in order to calculate the average grade in you class? Why? (the explanation is brief, you don’t need to write a paragraph.)
Answer:
Structure of arrays is much more efficient for storing grade data. As we discussed repeatedly in class, this is due to the fact that data is stored sequentially in computer memory. Therefore, it would be much easier for the computer to fetch data from memory when all grade data is stored in an array sequentially in memory, than when each grade is separated from the next student’s grade by their names, just as in array of structures.
7. Write a function getRoot() that takes in three coefficients $(a,b,c)$ of a quadratic equation $ax^2+bx+c$ and outputs the roots of this equation as the function output result.
Answer:
function [x1,x2] = getRoot(a,b,c)
d = sqrt(b^2 - 4*a*c);
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end
>> [r1,r2] = getRoot(1,1,1)
r1 =
-0.5000 + 0.8660i
r2 =
-0.5000 - 0.8660i
8. Write a MATLAB anonymous function that calculates the following integral, for arbitrary input integration limits $[a,b]$ and coefficient $c$,
Write your function such that it takes the three variables collectively as a structure.
Answer:
f = @(in) (integral(@(x) (x.^2 + in.c*x + 1),in.a,in.b));
9. Write a function getFac() that calculates the factorial of an input integer $n$ (no need for robust coding, assume the input variable is indeed a positive integer).
Answer:
function result=getFactorial(x)
if (x<=0)
result=1;
else
result=x*getFactorial(x-1);
end
end

