Random numbers in MATLAB
One of the most important topics in today’s science and computer simulation is random number generation and Monte Carlo simulation methods. In the simplest scenario for your research, you may need to generate a sequence of uniformly distributed random numbers in MATLAB. MATLAB has a large set of built-in functions to handle such random number generation problems. All of these functions are collectively named the statistics and machine learning toolbox in MATLAB.
MATLAB has a long list of random number generators. For example, you can use rand() to create a random number in the interval (0,1),
X = randreturns a single uniformly distributed random number in the interval (0,1).X = rand(n)returns an n-by-n matrix of random numbers.X = rand(n,m)returns an n-by-m matrix of random numbers.
For example, suppose you generated 10000 uniform random numbers,
>> RandomValues = rand(10000,1);
You could test whether the generated random numbers are truly uniformly distributed or not by plotting their histogram,
>> histogram(RandomValues)
which will plot the following figure,
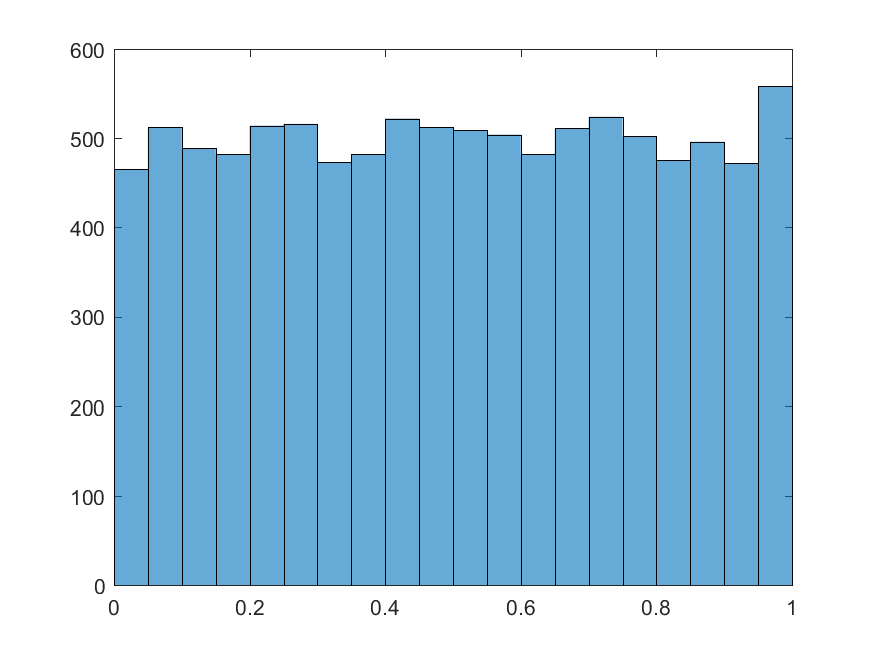
To generate random integer numbers in a given range, you can use randi() function,
– X = randi(imax) returns a pseudorandom scalar integer between 1 and imax.
– X = randi(imax,n) returns an n-by-n matrix of pseudorandom integers drawn from the discrete uniform distribution on the interval [1,imax].
– X = randi(imax,n,m) returns an n-by-m matrix of pseudorandom integers drawn from the discrete uniform distribution on the interval [1,imax].
– X = randi([imin,imax],n,m) an n-by-m matrix of pseudorandom integers drawn from the discrete uniform distribution on the interval [imin,imax].
For example,
>> randi([10 23], 3,2)
ans =
20 16
13 17
18 11
Note that so far, we have only generated uniformly distributed float/integer random numbers. We could, however, generate random numbers according to any distribution we wish, that is also supported by MATLAB. For example, a very popular distribution choice, is random number from the Normal (Gaussian) distribution. To get normally distributed random numbers, you can use MATLAB function randn(),
– X = randn returns a random scalar drawn from the standard normal distribution (mean=0,sigma=1).
– X = randn(n) returns an n-by-n matrix of standard-normally distributed random numbers.
– X = randn(n,m) returns an n-by-m matrix of standard-normally distributed random numbers.
Note that this function generated only standard-normally distributed random values. Therefore, a histogram of 10000 of such values produced by randn() would look something like the following,
>> SNormalValues = randn(10000,1);
>> histogram(SNormalValues);
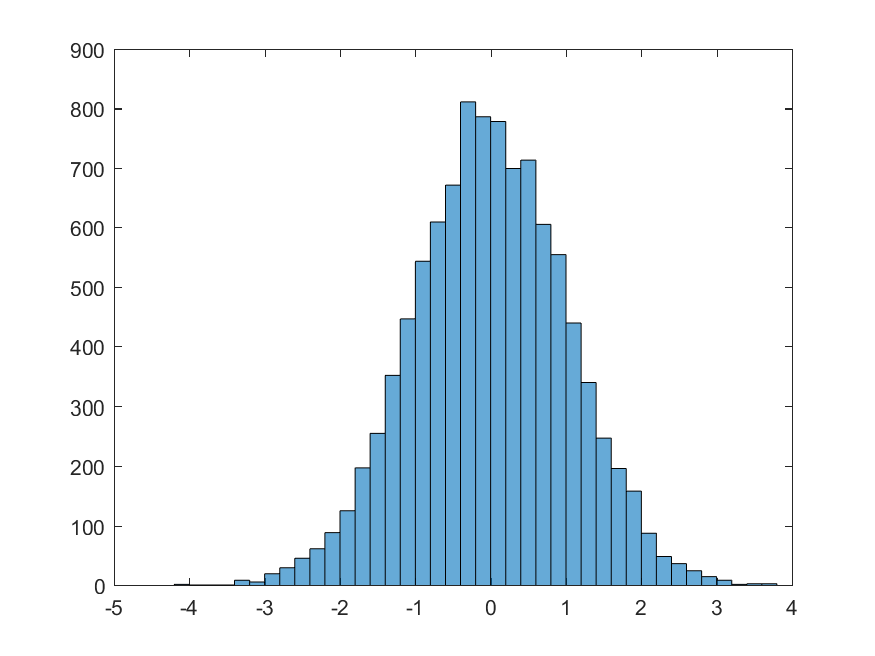
To get normally distributed random numbers with mean and standard deviation other than the standard normal distribution ($\mu=0,\sigma=1$), you will have to use another MATLAB builtin function normrnd(),
-
R = normrnd(mu,sigma) generates random numbers from the normal distribution with mean parameter mu and standard deviation parameter sigma. mu and sigma can be vectors, matrices, or multidimensional arrays that have the same size, which is also the size of R. A scalar input for mu or sigma is expanded to a constant array with the same dimensions as the other input.
-
R = normrnd(mu,sigma,m,n,…) or R = normrnd(mu,sigma,[m,n,…]) generates an m-by-n-by-… array. The mu, sigma parameters can each be scalars or arrays of the same size as R.
NormalValues = normrnd(100, 10, 10000, 1);
>> histogram(NormalValues)
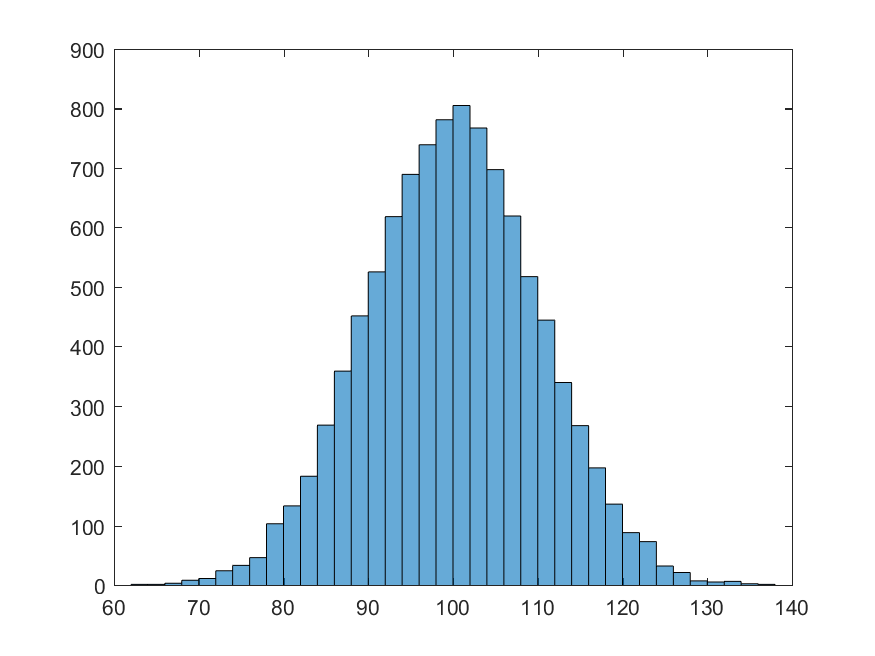
The deterministic aspect of randomness in MATLAB
There is a truth about random numbers and random number generators and algorithms, not only in MATLAB, but in all programming languages, and that is, true random numbers do not exist in the world of computer programming.
What we call a sequence of random numbers, is simply a sequence of numbers that we, the user, to the best of our knowledge, don’t know how it was generated, and therefore, the sequence looks random to us, but not the to the developer of the algorithm!. To prove this, type the following code in a MATLAB session,
>> rng(135);
>> rand()
ans =
0.8844
>> rand()
ans =
0.0771
>> rand()
ans =
0.5492
>> rand()
ans =
0.8296
Here, the function rng() controls the random number generation algorithm using the input positive integer number. The truth is that every algorithm for random number generation is deterministic and starts from an input integer number, called the seed of random number generator, to construct the sequence of random numbers. This means, that if we set the random number seed to a fixed value before we call the random number generator every time, then we will always get the same fixed random value (in fact, it is not random anymore!),
>> rng(135);
>> rand()
ans =
0.6613
>> rng(135);
>> rand()
ans =
0.6613
>> rng(135);
>> rand()
ans =
0.6613
>> rng(135);
>> rand()
ans =
0.6613
Note that, every time you restart MATLAB, the random number generator seed is set back to the default value, nor matter what you set it to in the last time. This means that every time you open MATLAB, type rand(), you will get the same random number as in the last time you opened MATLAB. To avoid this problem, you can use,
>> rng('shuffle')
which seeds the random number generator based on the current time in the CPU. Thus, rand, randi, and randn will produce a different sequence of numbers after each time you call rng(‘shuffle’).
Sometimes, however, this is not the desired behavior. For example, you want the results of your code to be reproducible. In those cases, it is good to initialize the seed of the random number generator in MATLAB to some pre-specified number, so that every time you run your code, you get the same result as before. To learn more about the seed of random number generators in MATLAB, visit this page.
Creating random permutation of numbers
There is a useful MATLAB function called randperm() that generates a random permutation of numbers for the user,
- p = randperm(n) returns a row vector containing a random permutation of the integers from 1 to n inclusive.
For example, if we wanted to get a sequence of random numbers within the range from 1 to a given maximum integer $n$, say $n=10$, in an arbitrary order, we could use this function,
>> randperm(10)
ans =
8 5 2 1 10 6 4 3 9 7
>> randperm(10)
ans =
4 8 1 3 10 2 5 7 9 6
>> randperm(10)
ans =
6 1 2 4 5 8 7 3 10 9
Note that every time you call the function, you would get a new random permutation of the requested sequence of numbers.