Suppose we did not know the value of $\pi$ and we wanted to estimate its value using Monte Carlo methods. One practical approach is to draw a square of unit side, with its diagonal opposite corners extending from the coordinates origin $(0,0)$ to $(1,1)$. Now we try to simulate uniform random points from inside of this square by generating uniform random points along the $X$ and $Y$ axes, i.e., by generating two random uniform numbers (x,y) from the range $[0,1]$.
Now the generated random point $P$ has the coordinate $(x,y)$, so we can calculate its distance from the coordinate origin. Now suppose we also draw a quarter-circle inside of this square whose radius is unit and is centered at the origin $(0,0)$. The ratio of the area of this quarter-circle, $S_C$ to the area of the square enclosing it, $S_S$ is,
\[\frac{S_C}{S_S} = \frac{\frac{1}{4}\pi r^2}{r^2} = \frac{1}{4}\pi\]This is because the area of the square of unit-length sides is just 1. Therefore, if we can somehow measure the area of the quarter $S_C$, then we can use the following equation, to get an estimate of $\pi$,
\[\pi = 4S_C\]To obtain, $S_C$, we are going to throw random points in the square, just as described above, and then find the fraction of points, $f=n_C/n_{\rm total}$, that fall inside this quarter-circle. This fraction is related to the area of the circle and square by the following equation,
\[f=\frac{n_C}{n_{\rm total}} = \frac{S_C}{S_S}\]Therefore, one can obtain an estimate of $\pi$ using this fraction,
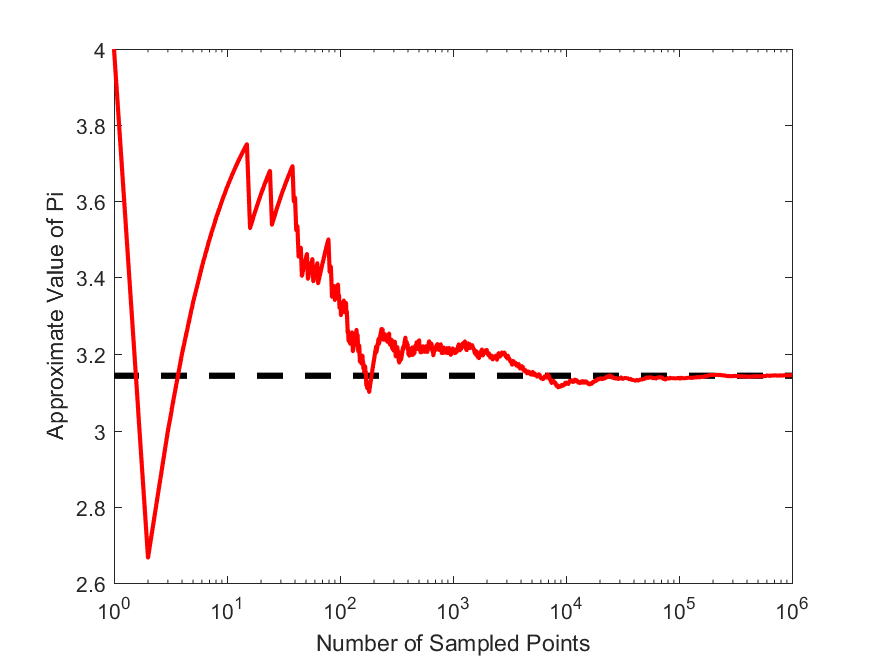
\[\pi \approx 4\frac{n_C}{n_{\rm total}}\]Now, write a script that takes in the number of points to be simulated, and then calculates an approximate value for $\pi$ based on the Monte Carlo algorithm described above. Write a second function that plot the estimate of $\pi$ versus the number of points stimulated, like the following,