Supposed we have observed a dataset of events with one attribute variable in this file: data.csv. Plotting these points would yield a blue-colored histogram like the following plot,
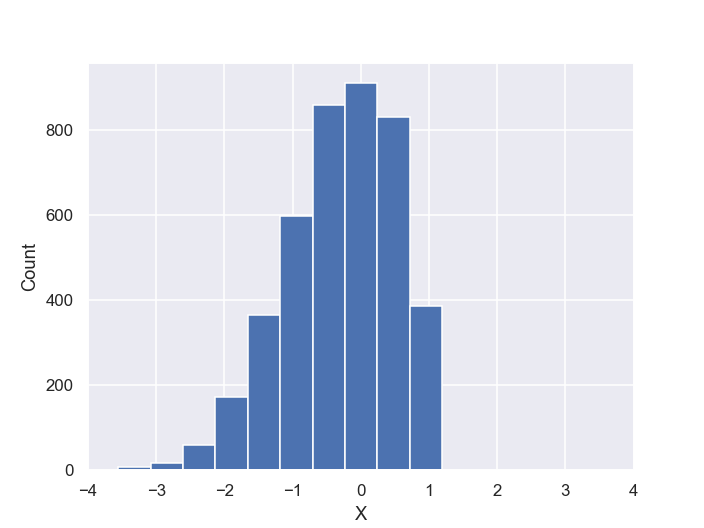
Unlike the previous problems where the censorship was due to a sharp cutoff on a Gaussian dataset, the smooth cutoff in this problem is due to the following Gaussian model mixed with and inverted Gaussian CDF,
\[\pi( x | \mu_G, \sigma_G, \mu_C, \sigma_C) \propto \mathcal{N}(x | \mu_G, \sigma_G) \times \frac{1}{2} \Big[ 1 + \text{erf}\Big(\frac{\mu_C-x}{\sigma_C\sqrt{2}}\Big) \Big] ~,\]where $\mu_G, \sigma_G$ are the mean and standard deviation parameters of the Gaussian distribution and $\mu_G, \sigma_G$ are the unknown parameters of the Gaussian CDF smooth cutoff on this dataset.
Now our goal is to constrain the four unknown parameters of the above model using the maximum likelihood method. You can use the ParaMonte library in Python or in MATLAB to explore the resulting log-likelihood function. In such s case, make sure you start your MCMC exploration by a good set of initial parameter values, such that the MCMC sampler can correctly explore the parameter-space without getting lost. You can get help from another relevant problem here.

