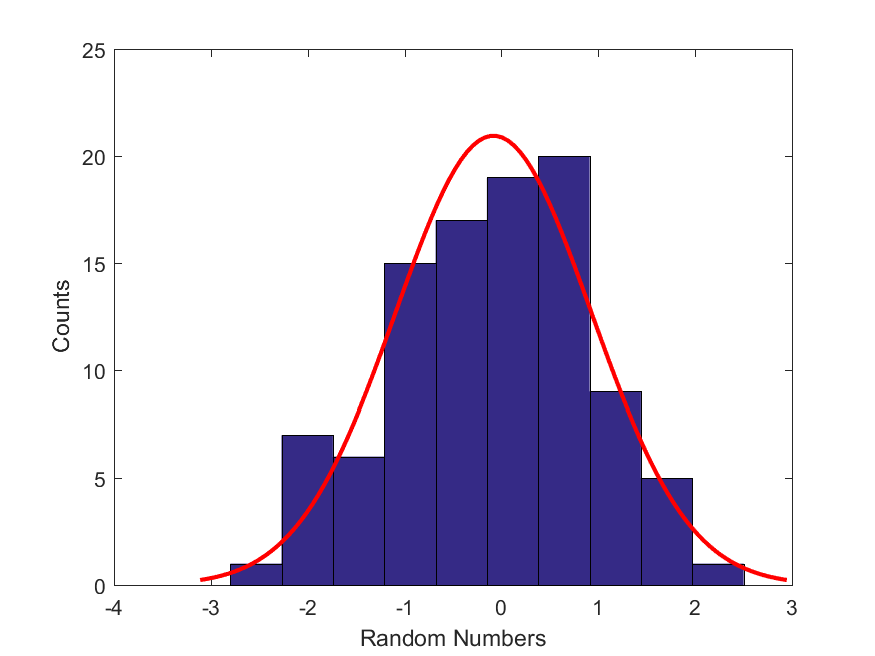
Consider this dataset, Drand.mat, which contains a set of random numbers. Let’s make a hypothesis with regards to this dataset: We assume that this dataset is well fit by a Gaussian distribution. But, we don’t know the values of the two parameters (mean and standard deviation) of this Normal (Gaussian) distribution.
Write a script that constructs a mathematical objective function and then use an optimization algorithm of your choice to find the most likely values of the mean and standard deviation of this Gaussian distribution. Here is a best-fit Gaussian distribution using the most likely parameters to the histogram of this dataset.
Tip: Our hypothesis is that the data in this histogram comes from a standard Normal distribution with a fixed mean ($\mu$) and standard deviation ($\sigma$). For the moment, let’s assume that we know the values of these two parameters. Then if all of these points, $D$, come from the normal distribution with the given $(\mu,\sigma)$, then the probability of all them coming from the normal distribution with these parameter values can be computed as,
\(\pi\big(\boldsymbol D\big|\mu,\sigma\big) = \prod^{N=100}_{i=1} \frac{1}{2\pi\sigma^2}\exp\bigg( -\bigg[ \frac{\boldsymbol D(i)-\mu}{\sqrt{2}\sigma} \bigg]^2 \bigg) ~~,\)
where the symbol $\pi$ to the left of equality means probability (but note that $\pi$ on the right hand side of the euqation stands for the number $\pi=3.14\ldots$, and $D(i)$ refers to the $i$th point in the sample of points. Since probabilities are always extremely small numbers, it is always good to work with their log() values instead of their raw values (can you guess why?). Therefore, we could take the log of the above equation to write it as,
\(\log\pi\big(\boldsymbol D\big|\mu,\sigma\big) = \sum^{N=100}_{i=1} - \log\big(2\pi\sigma^2\big) - \bigg[ \frac{\boldsymbol D(i)-\mu}{\sqrt{2}\sigma} \bigg]^2 ~~,\)
Now our goal is to construct this function (let’s name it getLogProbNorm()) and pass it to an optimizer to find the most likely $(\mu,\sigma)$ that leads to the highest likelihood value (the maximum of the above equation).
Tip: For optimization tasks in MATLAB, you can use MATLAB’s built-in function, fminsearch(). Note that fminsearch() minimizes functions, but here we want to maximize getLogProbNorm(), instead of minimizing it. What change could you make to this function to make it work with fminsearch()?
Name your main script findBestFitParameters.m. Now when you run your script it should call fminsearch() and then output the best-fit parameters like the following,
>> findBestFitParameters
mu: -0.082001 , sigma: 1.0043
Start your parameter search via fminsearch() with the following values: $[\mu,\sigma] = [1,10]$.
Tip:
For optimization tasks in Python, you can use fmin() function from Python’s package scipy: from scipy.optimize import fmin. To read MATLAB binary files (*.mat) in Python, you will have to use Scipy’s loadmat() function (from scipy.io import loadmat).
Name your main script findBestFitParameters.py. Here is an example expected output of such script,
findBestFitParameters
Optimization terminated successfully.
Current function value: 142.326191
Iterations: 50
Function evaluations: 98
mean = -0.08200050180312446, standard-deviation = 1.0043358235352169
Start your parameter search via fmin() with the following values: $[\mu,\sigma] = [1,10]$.