Recall that computers can only store discrete values in memory.
- What does this imply for the storage of real (floating-point) numbers in computers?
- Now consider the IEEE-storage convention for real numbers in computers for
real32,real64, andreal128bit storage formats as illustrated below.
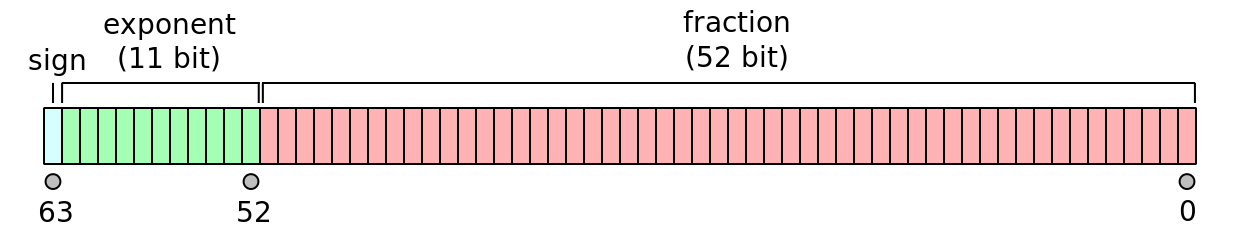

Compute how many real numbers each of the above formats can represent.
- How many of these numbers are in the range $[0, 1)$ for each storage convention?
- What are the minimum and maximum possible representable real values in these conventions?
- Is there a way to represent numbers that are smaller than the minimum representable real numbers in these conventions?

