Consider this dataset, Drand.mat, which contains a set of random numbers. Write a sctipt that computes the mean of this sample via the Least-Sum-of-Squares method. For this, you will need to use a funtion minimizer in the language of your choice. Compare your results in the end with the simple method of computing the mean, which is the sum of all the values divided by the number of points.
Here is a best-fit Gaussian distribution using the most likely parameters to the histogram of this dataset.
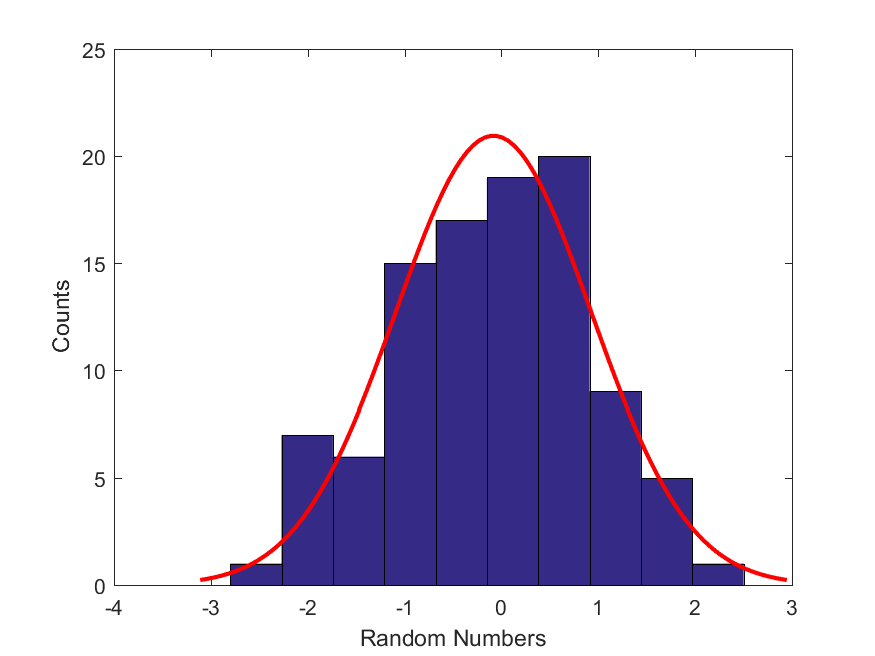
Tip:
For optimization tasks in Python, you can use fmin() function from Python’s package scipy: from scipy.optimize import fmin. To read MATLAB binary files (*.mat) in Python, you will have to use Scipy’s loadmat() function (from scipy.io import loadmat).
Name your main script findBestFitParameters.py. Here is an example expected output of such script,
findBestFitParameters.py
Optimization terminated successfully.
Current function value: 100.868424
Iterations: 21
Function evaluations: 42
Least-Squares mean = -0.08197021484375
simple average formula = -0.08197189633971344
relative difference = 2.0513289127509662e-05
Start your parameter search via fmin() with the following value: $\mu = 10$.


