3D-plotting in matplotlib
Over the past few years matplotlib has significantly grown to include additional plotting capabilities including 3D plotting techniques. At this point in the Python learning process, it is generally more sensible to learn the latest techniques of the advanced Python packages (including matplotlib) directly from their reference manual. The reason for this is that the interfaces for many of these packages are constantly evolving and any code that may work today, may not be functional in a few months or years. With this note in mind, the following is a quick overview of some of these plotting functionalities.
%matplotlib notebook to the beginning of your Jupyter notebook. This IPython magic will make all the plots that will be generated in the notebook interactive, meaning that you will be able to zoom in and out, resize, or rotate the plots inside the notebook.
Creating 3D figure objects
To generate 3D figures, you will have to import mpl_toolkits Python package,
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes(projection="3d")
plt.show()
This should generate the following figure handle for you,
To save the plot in an external file, use the savefig() method.
plt.savefig('emptyFigure3D.png')
Creating 3D line plots
Now suppose we want to visualize a 3D line which is described by the following equations,
import numpy as np
zmin = 0.0
zmax = 4*np.pi
LineZ = np.linspace(zmin, zmax, 500)
LineY = np.sin(LineZ)
LineX = np.cos(LineZ)
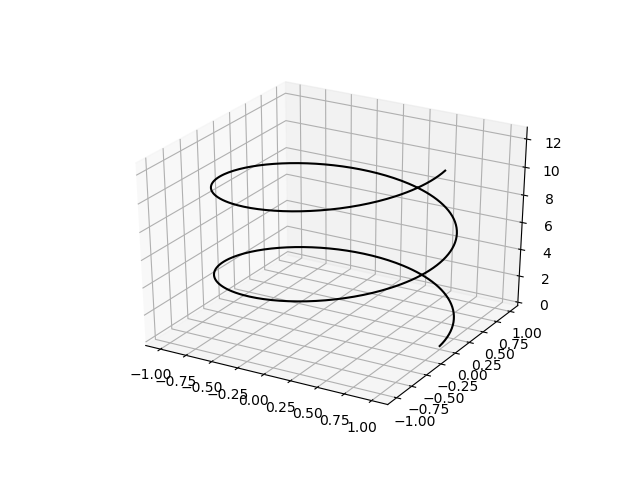
If you look carefully, you may notice that the X and Y coordinates described by the above equations describe a circular, repeating, line. On the contrary, the Z coordinates are described by a set of monotonically increasing values. Therefore, this 3D line must be describing a spring-like object. To plot this object, we can use the following,
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes(projection="3d")
ax.plot3D( x_line, y_line, z_line, 'gray')
plt.show()
plt.savefig('line3D.png')
which would give a plot like the following,
Creating 3D scatter plots
Now, suppose we want to add a set of points to this line plot. For example, we could create a set of random points around the 3D line and visualize them, as if the random points are a set of observational data and the 3D line represents a mathemtical fit to this observational dataset,
import numpy as np
nPoint = 300 # number of random points
PointZ = zmin + (zmax-zmin) * np.random.random(nPoint) # points have uniformly-distributed random heights along the Z axis
PointY = np.sin(PointZ) + 0.1 * np.random.randn(nPoint) # points have normally-distributed random values along the Y axis
PointX = np.cos(PointZ) + 0.1 * np.random.randn(nPoint) # points have normally-distributed random values along the X axis
ax.scatter3D( PointX, PointY, PointZ
, c=PointZ # color value of individual points is taken from their heights
, cmap="hsv" # the color mapping to be used. Other example options: winter, autumn, ...
);
plt.show()
plt.savefig('lineScatter3D.png')
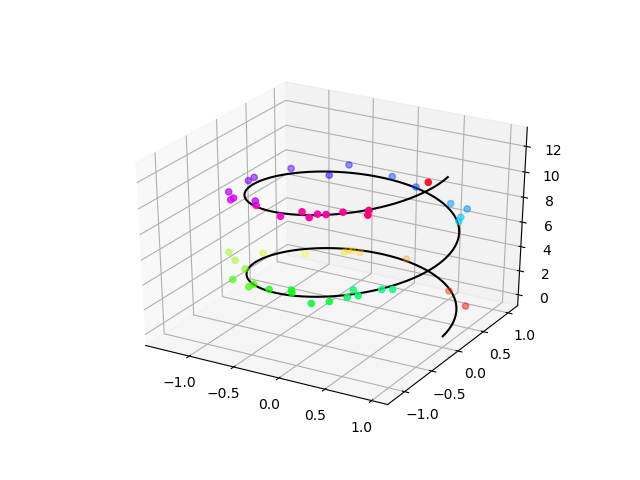
To get a full list of all color-maps that you can use and information about them, try,
help(plt.colormaps)
Help on function colormaps in module matplotlib.pyplot:
colormaps()
Matplotlib provides a number of colormaps, and others can be added using
:func:`~matplotlib.cm.register_cmap`. This function documents the built-in
colormaps, and will also return a list of all registered colormaps if
called.
You can set the colormap for an image, pcolor, scatter, etc,
using a keyword argument::
imshow(X, cmap=cm.hot)
or using the :func:`set_cmap` function::
imshow(X)
pyplot.set_cmap('hot')
pyplot.set_cmap('jet')
In interactive mode, :func:`set_cmap` will update the colormap post-hoc,
allowing you to see which one works best for your data.
All built-in colormaps can be reversed by appending ``_r``: For instance,
``gray_r`` is the reverse of ``gray``.
There are several common color schemes used in visualization:
Sequential schemes
for unipolar data that progresses from low to high
Diverging schemes
for bipolar data that emphasizes positive or negative deviations from a
central value
Cyclic schemes
for plotting values that wrap around at the endpoints, such as phase
angle, wind direction, or time of day
Qualitative schemes
for nominal data that has no inherent ordering, where color is used
only to distinguish categories
Matplotlib ships with 4 perceptually uniform color maps which are
the recommended color maps for sequential data:
========= ===================================================
Colormap Description
========= ===================================================
inferno perceptually uniform shades of black-red-yellow
magma perceptually uniform shades of black-red-white
plasma perceptually uniform shades of blue-red-yellow
viridis perceptually uniform shades of blue-green-yellow
========= ===================================================
The following colormaps are based on the `ColorBrewer
<http://colorbrewer2.org>`_ color specifications and designs developed by
Cynthia Brewer:
ColorBrewer Diverging (luminance is highest at the midpoint, and
decreases towards differently-colored endpoints):
======== ===================================
Colormap Description
======== ===================================
BrBG brown, white, blue-green
PiYG pink, white, yellow-green
PRGn purple, white, green
PuOr orange, white, purple
RdBu red, white, blue
RdGy red, white, gray
RdYlBu red, yellow, blue
RdYlGn red, yellow, green
Spectral red, orange, yellow, green, blue
======== ===================================
ColorBrewer Sequential (luminance decreases monotonically):
======== ====================================
Colormap Description
======== ====================================
Blues white to dark blue
BuGn white, light blue, dark green
BuPu white, light blue, dark purple
GnBu white, light green, dark blue
Greens white to dark green
Greys white to black (not linear)
Oranges white, orange, dark brown
OrRd white, orange, dark red
PuBu white, light purple, dark blue
PuBuGn white, light purple, dark green
PuRd white, light purple, dark red
Purples white to dark purple
RdPu white, pink, dark purple
Reds white to dark red
YlGn light yellow, dark green
YlGnBu light yellow, light green, dark blue
YlOrBr light yellow, orange, dark brown
YlOrRd light yellow, orange, dark red
======== ====================================
ColorBrewer Qualitative:
(For plotting nominal data, :class:`ListedColormap` is used,
not :class:`LinearSegmentedColormap`. Different sets of colors are
recommended for different numbers of categories.)
* Accent
* Dark2
* Paired
* Pastel1
* Pastel2
* Set1
* Set2
* Set3
A set of colormaps derived from those of the same name provided
with Matlab are also included:
========= =======================================================
Colormap Description
========= =======================================================
autumn sequential linearly-increasing shades of red-orange-yellow
bone sequential increasing black-white color map with
a tinge of blue, to emulate X-ray film
cool linearly-decreasing shades of cyan-magenta
copper sequential increasing shades of black-copper
flag repetitive red-white-blue-black pattern (not cyclic at
endpoints)
gray sequential linearly-increasing black-to-white
grayscale
hot sequential black-red-yellow-white, to emulate blackbody
radiation from an object at increasing temperatures
jet a spectral map with dark endpoints, blue-cyan-yellow-red;
based on a fluid-jet simulation by NCSA [#]_
pink sequential increasing pastel black-pink-white, meant
for sepia tone colorization of photographs
prism repetitive red-yellow-green-blue-purple-...-green pattern
(not cyclic at endpoints)
spring linearly-increasing shades of magenta-yellow
summer sequential linearly-increasing shades of green-yellow
winter linearly-increasing shades of blue-green
========= =======================================================
A set of palettes from the `Yorick scientific visualisation
package <https://dhmunro.github.io/yorick-doc/>`_, an evolution of
the GIST package, both by David H. Munro are included:
============ =======================================================
Colormap Description
============ =======================================================
gist_earth mapmaker's colors from dark blue deep ocean to green
lowlands to brown highlands to white mountains
gist_heat sequential increasing black-red-orange-white, to emulate
blackbody radiation from an iron bar as it grows hotter
gist_ncar pseudo-spectral black-blue-green-yellow-red-purple-white
colormap from National Center for Atmospheric
Research [#]_
gist_rainbow runs through the colors in spectral order from red to
violet at full saturation (like *hsv* but not cyclic)
gist_stern "Stern special" color table from Interactive Data
Language software
============ =======================================================
A set of cyclic color maps:
================ =================================================
Colormap Description
================ =================================================
hsv red-yellow-green-cyan-blue-magenta-red, formed by
changing the hue component in the HSV color space
twilight perceptually uniform shades of
white-blue-black-red-white
twilight_shifted perceptually uniform shades of
black-blue-white-red-black
================ =================================================
Other miscellaneous schemes:
============= =======================================================
Colormap Description
============= =======================================================
afmhot sequential black-orange-yellow-white blackbody
spectrum, commonly used in atomic force microscopy
brg blue-red-green
bwr diverging blue-white-red
coolwarm diverging blue-gray-red, meant to avoid issues with 3D
shading, color blindness, and ordering of colors [#]_
CMRmap "Default colormaps on color images often reproduce to
confusing grayscale images. The proposed colormap
maintains an aesthetically pleasing color image that
automatically reproduces to a monotonic grayscale with
discrete, quantifiable saturation levels." [#]_
cubehelix Unlike most other color schemes cubehelix was designed
by D.A. Green to be monotonically increasing in terms
of perceived brightness. Also, when printed on a black
and white postscript printer, the scheme results in a
greyscale with monotonically increasing brightness.
This color scheme is named cubehelix because the r,g,b
values produced can be visualised as a squashed helix
around the diagonal in the r,g,b color cube.
gnuplot gnuplot's traditional pm3d scheme
(black-blue-red-yellow)
gnuplot2 sequential color printable as gray
(black-blue-violet-yellow-white)
ocean green-blue-white
rainbow spectral purple-blue-green-yellow-orange-red colormap
with diverging luminance
seismic diverging blue-white-red
nipy_spectral black-purple-blue-green-yellow-red-white spectrum,
originally from the Neuroimaging in Python project
terrain mapmaker's colors, blue-green-yellow-brown-white,
originally from IGOR Pro
============= =======================================================
The following colormaps are redundant and may be removed in future
versions. It's recommended to use the names in the descriptions
instead, which produce identical output:
========= =======================================================
Colormap Description
========= =======================================================
gist_gray identical to *gray*
gist_yarg identical to *gray_r*
binary identical to *gray_r*
========= =======================================================
.. rubric:: Footnotes
.. [#] Rainbow colormaps, ``jet`` in particular, are considered a poor
choice for scientific visualization by many researchers: `Rainbow Color
Map (Still) Considered Harmful
<http://ieeexplore.ieee.org/document/4118486/?arnumber=4118486>`_
.. [#] Resembles "BkBlAqGrYeOrReViWh200" from NCAR Command
Language. See `Color Table Gallery
<https://www.ncl.ucar.edu/Document/Graphics/color_table_gallery.shtml>`_
.. [#] See `Diverging Color Maps for Scientific Visualization
<http://www.kennethmoreland.com/color-maps/>`_ by Kenneth Moreland.
.. [#] See `A Color Map for Effective Black-and-White Rendering of
Color-Scale Images
<https://www.mathworks.com/matlabcentral/fileexchange/2662-cmrmap-m>`_
by Carey Rappaport
Creating 3D wire plots
Now suppose we have a 3D mathematical function that defines a surface in 3D, such as the following,
import numpy as np
def getZ(X, Y):
return np.sin(np.sqrt(X ** 2 + Y ** 2))
X = np.linspace(-5, 5, 40)
Y = np.linspace(-5, 5, 40)
X, Y = np.meshgrid(X, Y)
Z = getZ(X, Y)
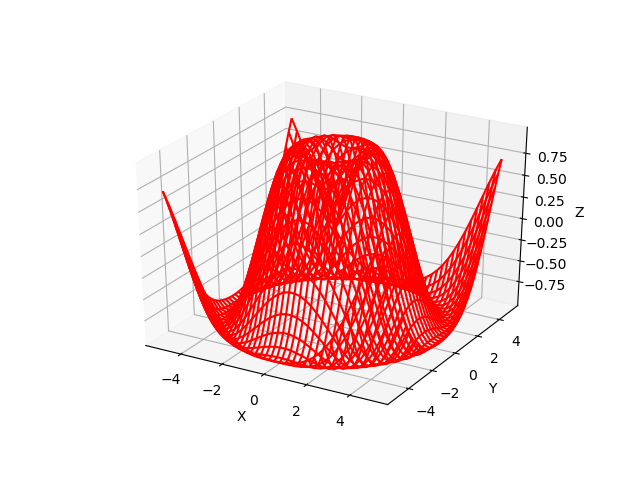
With the three mesh grids (X,Y,Z) generated in the above, we can now visualize this 3D function via a wire plot like the following,
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes(projection="3d")
ax.plot_wireframe(X, Y, Z, color='red')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()
plt.savefig('wire3D.png')
which will generate the following plot,
Creating 3D surface plots
Now suppose we want to visualize the surface of the same function as in the case of the wire plot,
import numpy as np
def getZ(X, Y):
return np.sin(np.sqrt(X ** 2 + Y ** 2))
X = np.linspace(-5, 5, 40)
Y = np.linspace(-5, 5, 40)
X, Y = np.meshgrid(X, Y)
Z = getZ(X, Y)
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes(projection="3d")
ax.plot_surface (X, Y, Z
, rstride=1 # default value is one
, cstride=1 # default value is one
, cmap='winter'
, edgecolor='none'
)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Surface Plot');
plt.show()
plt.savefig('surface3D.png')
This will generate the following plot,
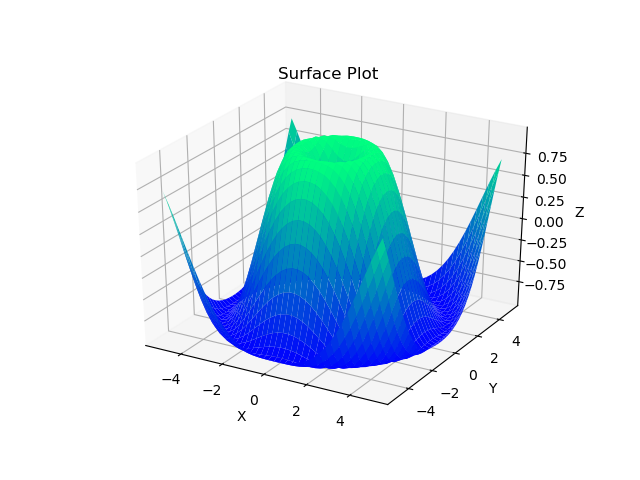
However, you may have noticed that this plot looks very coarse. To refine the image, we can increase the number of grids in the 3D mesh that we generate for the visualization. Instead of using 40 grids as used previously, we will use a larger number, for example, 300,
import numpy as np
def getZ(X, Y):
return np.sin(np.sqrt(X ** 2 + Y ** 2))
X = np.linspace(-5, 5, 300)
Y = np.linspace(-5, 5, 300)
X, Y = np.meshgrid(X, Y)
Z = getZ(X, Y)
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes(projection="3d")
ax.plot_surface (X, Y, Z
, rstride=1 # default value is one
, cstride=1 # default value is one
, cmap='winter'
, edgecolor='none'
)
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
ax.set_title('Fine-Mesh Surface Plot');
plt.show()
plt.savefig('refinedSurface3D.png')
The resulting surface plot now looks much more refined and pleasant,
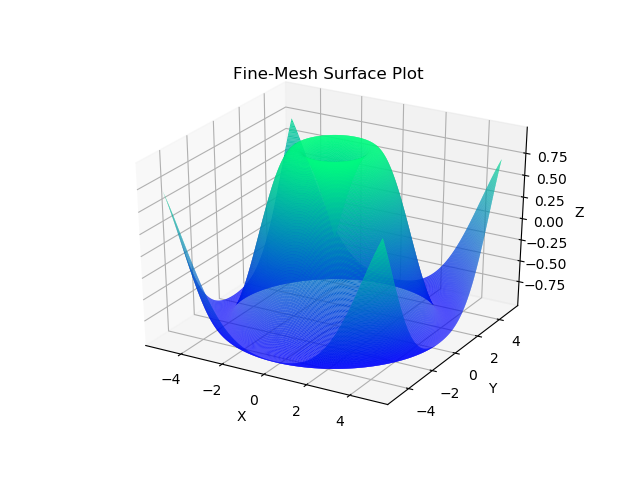
Creating contour plots
The 3D surface or wire plots have limited usage because of their difficult interpretations, especially when they presented as fixed static images as opposed to interactive live plots. A more useful 3D plotting technique, in particular, for scientific reports is the contour plotting. Suppose we have a very weird-looking 3D function which is hard to visualize via a surface plot,
import numpy as np
def func(x, y):
return np.sin(x) ** 5 + np.cos(10 + y * x) * np.cos(x)
We can visualize this function via a contour plot by creating mesh grid of the coordinates again,
import numpy as np
def func(X, Y):
return np.sin(X) ** 5 + np.cos(10 + Y * X) * np.cos(X)
X = np.linspace(0, 2*np.pi, 500)
Y = np.linspace(0, 2*np.pi, 500)
X, Y = np.meshgrid(X, Y)
Z = func(X, Y)
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes()
ax.contour(X, Y, Z, colors='gray');
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
plt.savefig('contour.png')
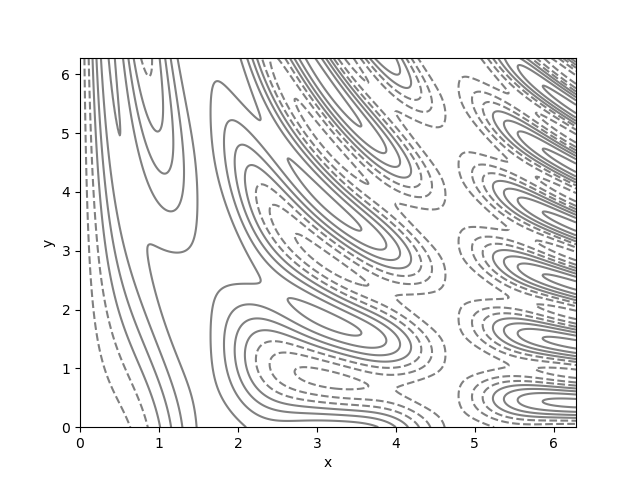
We could also change the color from uniform gray to a more descriptive color-map instead,
import numpy as np
def func(X, Y):
return np.sin(X) ** 5 + np.cos(10 + Y * X) * np.cos(X)
X = np.linspace(0, 2*np.pi, 500)
Y = np.linspace(0, 2*np.pi, 500)
X, Y = np.meshgrid(X, Y)
Z = func(X, Y)
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes()
ax.contour (X, Y, Z
, cmap = 'RdGy'
);
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
plt.savefig('contourColorMap.png')
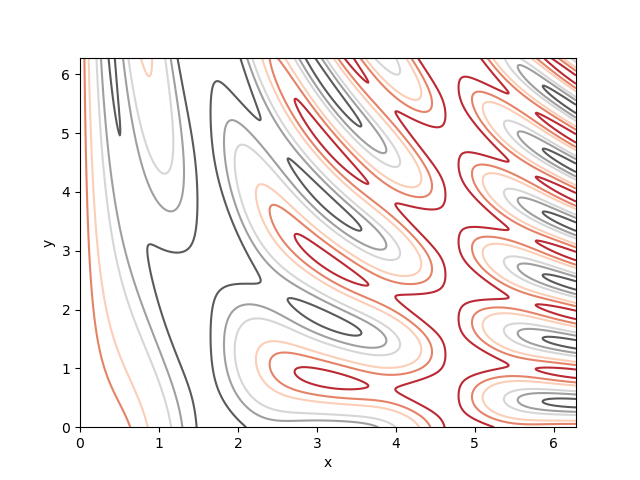
or perhaps autumn color-map,
import numpy as np
def func(X, Y):
return np.sin(X) ** 5 + np.cos(10 + Y * X) * np.cos(X)
X = np.linspace(0, 2*np.pi, 500)
Y = np.linspace(0, 2*np.pi, 500)
X, Y = np.meshgrid(X, Y)
Z = func(X, Y)
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes()
ax.contour (X, Y, Z
, cmap = plt.cm.autumn
);
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
plt.savefig('contourColorMapAutumn.png')
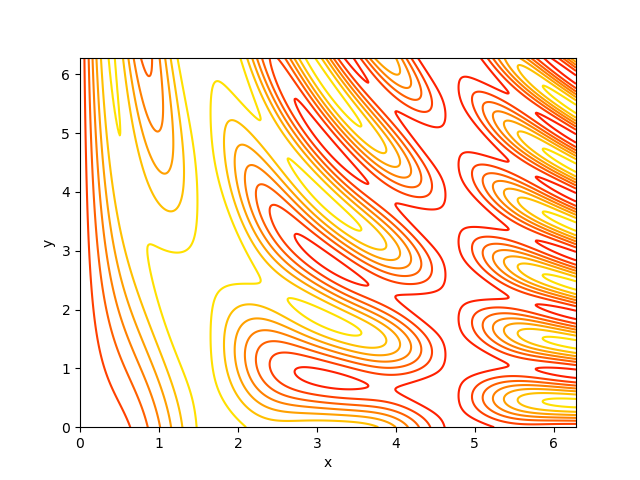
Creating filled contour plots
But what if we are interested not in contour lines, but an overall behavior of the function everywhere, womething like a heat-map? There is the contourf() method there to help us,
import numpy as np
def func(X, Y):
return np.sin(X) ** 5 + np.cos(10 + Y * X) * np.cos(X)
X = np.linspace(0, 2*np.pi, 500)
Y = np.linspace(0, 2*np.pi, 500)
X, Y = np.meshgrid(X, Y)
Z = func(X, Y)
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes()
ax.contourf (X, Y, Z
, 20 # the number of color levels in the heat-map
, cmap = "RdGy"
);
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
plt.savefig('contourf.png')
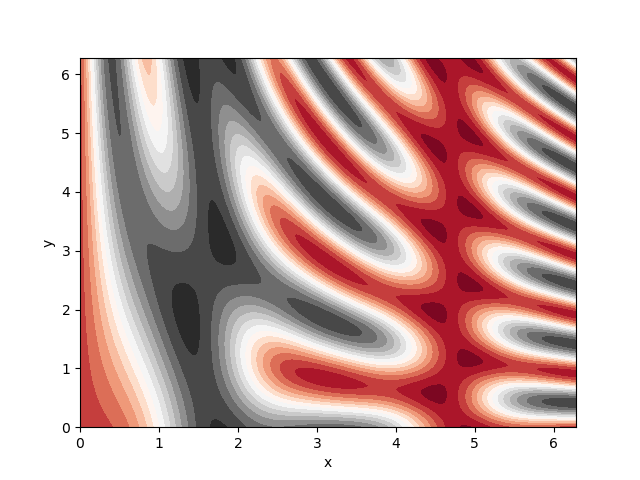
You may again notice the low-resolution of the plot. To refine the plot, we can increase the number of color-levels in the plot, for example to 100 from 20,
import numpy as np
def func(X, Y):
return np.sin(X) ** 5 + np.cos(10 + Y * X) * np.cos(X)
X = np.linspace(0, 2*np.pi, 500)
Y = np.linspace(0, 2*np.pi, 500)
X, Y = np.meshgrid(X, Y)
Z = func(X, Y)
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes()
ax.contourf (X, Y, Z
, 100 # the number of color levels in the heat-map
, cmap = "RdGy"
);
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
plt.savefig('contourfRefined.png')
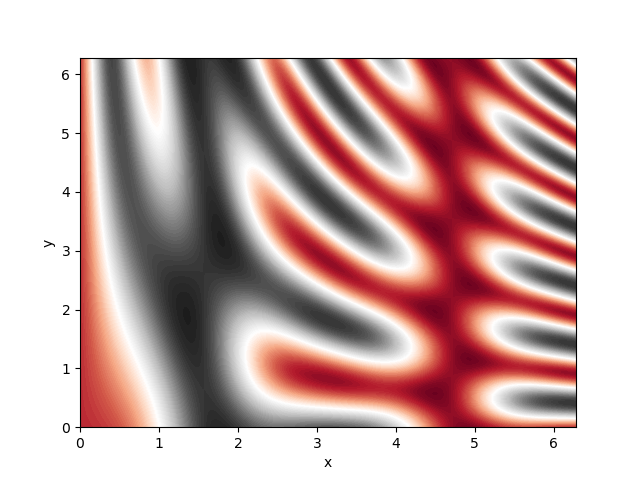
However, refining filled contour plots by increasing the number of color levels could affect the performance of our script. Another way to achieve the same goal is to use another plotting method called imshow() instead of contourf(),
import numpy as np
def func(X, Y):
return np.sin(X) ** 5 + np.cos(10 + Y * X) * np.cos(X)
X = np.linspace(0, 2*np.pi, 500)
Y = np.linspace(0, 2*np.pi, 500)
X, Y = np.meshgrid(X, Y)
Z = func(X, Y)
%matplotlib notebook
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
fig = plt.figure()
ax = plt.axes()
plt.imshow( Z
, extent=[0, 2*np.pi, 0, 2*np.pi] # doesn't accept X and Y grids, so you must manually specify the extent [xmin, xmax, ymin, ymax] of the image on the plot
, origin='lower' # default origin of the plot is the upper-left
, cmap='RdGy'
)
plt.colorbar()
ax.set_xlabel('x')
ax.set_ylabel('y')
plt.show()
plt.savefig('imshow.png')
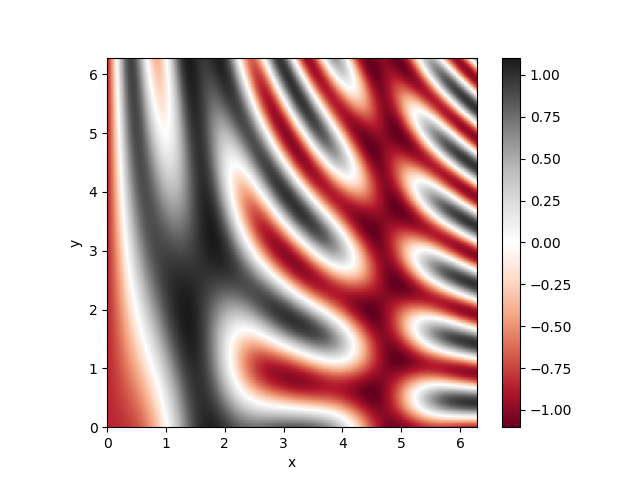
Notice the additional color bar that we have added to the above plot via the command plt.colorbar().